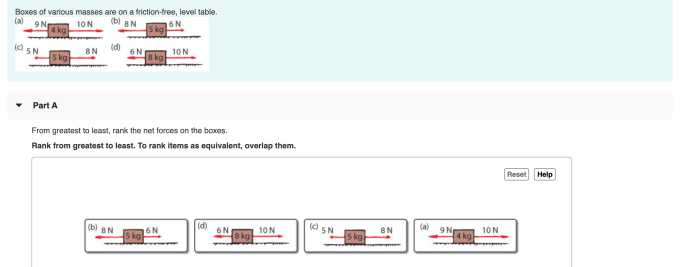
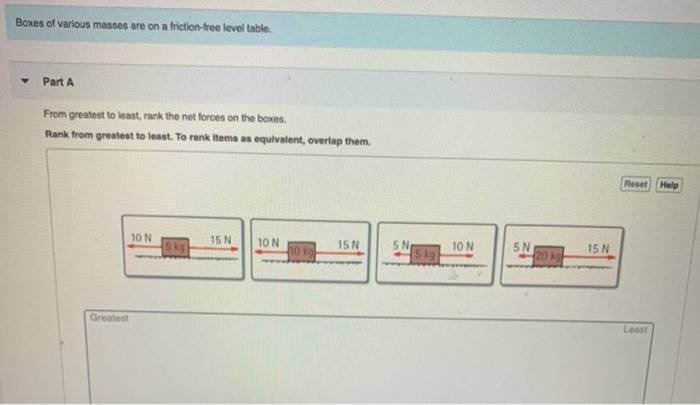
Boxes of various masses are on a friction-free level table, a captivating scenario that invites us to delve into the realm of physics. This exploration unveils the interplay of static and kinetic friction, Newton’s laws of motion, energy conservation, impulse and momentum, and collisions, providing a comprehensive understanding of the dynamics governing the motion of these objects.
As the boxes interact on this frictionless surface, they become a living laboratory, showcasing the fundamental principles that shape our physical world. We will witness how these principles govern the acceleration, velocity, and displacement of the boxes, unraveling the intricate dance of energy conversion and momentum exchange.
Static and Kinetic Friction: Boxes Of Various Masses Are On A Friction-free Level Table
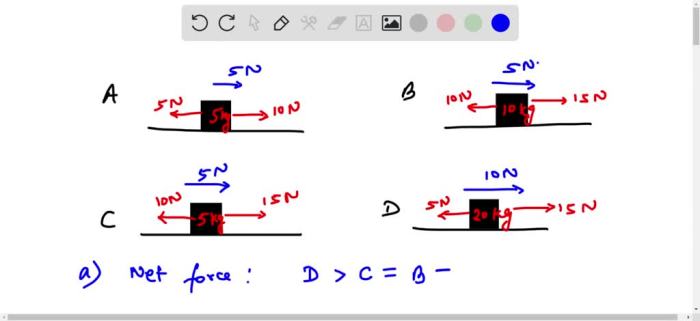
On a frictionless surface, boxes experience no resistance to movement. Static friction is the force that prevents an object from moving when a force is applied. Kinetic friction is the force that opposes the motion of an object once it has started moving.
For example, if a box is sitting on a frictionless surface and a force is applied to it, the box will start to move immediately. This is because there is no static friction to prevent the box from moving. However, if the surface is not frictionless, then the box will experience static friction.
This will prevent the box from moving until the force applied to it is greater than the force of static friction.
Newton’s Laws of Motion
Newton’s laws of motion describe the relationship between an object’s mass, velocity, and the forces acting on it. The first law states that an object at rest will remain at rest unless acted on by an unbalanced force. The second law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
The third law states that for every action, there is an equal and opposite reaction.
These laws can be used to calculate the acceleration, velocity, and displacement of the boxes. For example, if a box is pushed with a force of 10 N and has a mass of 2 kg, then its acceleration will be 5 m/s^2.
Its velocity will increase by 5 m/s every second, and its displacement will be 2.5 m after 1 second.
Energy Conservation
The law of conservation of energy states that the total energy of a system remains constant. This means that the potential energy of the boxes is converted into kinetic energy as they move.
For example, if a box is lifted to a height of 1 m and then released, it will have a potential energy of 9.8 J. As the box falls, its potential energy is converted into kinetic energy. By the time it reaches the ground, all of its potential energy has been converted into kinetic energy.
Impulse and Momentum, Boxes of various masses are on a friction-free level table
Impulse is the product of force and time. Momentum is the product of mass and velocity. The law of conservation of momentum states that the total momentum of a system remains constant.
For example, if a box with a mass of 2 kg is moving with a velocity of 3 m/s and collides with a box with a mass of 1 kg that is at rest, the total momentum of the system is 6 kg m/s.
After the collision, the two boxes will move together with a velocity of 2 m/s.
Collisions
There are two types of collisions: elastic collisions and inelastic collisions. In an elastic collision, the total kinetic energy of the system is conserved. In an inelastic collision, some of the kinetic energy of the system is lost.
The laws of conservation of momentum and energy can be used to analyze collisions. For example, if two boxes with equal masses collide head-on with equal velocities, they will bounce off each other with the same velocities.
FAQ
What is the significance of friction in this scenario?
Friction is absent in this scenario, creating an ideal environment to study the motion of objects without the influence of frictional forces.
How do Newton’s laws govern the motion of the boxes?
Newton’s laws provide a framework to calculate the acceleration, velocity, and displacement of the boxes based on the forces acting upon them.
What is the role of energy conservation in this system?
Energy conservation ensures that the total mechanical energy of the system remains constant, allowing us to track the conversion between potential and kinetic energy.